Global Scaling
from Dr. rer. net. Hartmut Müller
This is an introduction for people who are interested
Institut Space-Energy-Research in Wolfratsthausen, Director:
Dr. Hartmut Müller
An Introduction to Global-Scaling-Theory
 by Dr. rer. nat. Hartmut Müller, director of the Institute For Space-Energy-Research in memory of Leonard Euler (IREF), Wolfratshausen by Dr. rer. nat. Hartmut Müller, director of the Institute For Space-Energy-Research in memory of Leonard Euler (IREF), Wolfratshausen
Nature continues to amaze us with an almost infinite variety of phenomena. Man has been searching for centuries to find the principle that “holds the world inside together”. Today we are closer to the solution of this puzzle than never before.
The “Sacrament” of Physical Measuring
From the time of Galileo and Newton we have known and studied properties that are common to all material phenomena: space, time and motion. These are physical properties, which explains why physics holds a fundamental position among all of the natural sciences. Till the end of the 20th century physics dealt with the exploration of quantitative relationship between these fundamental properties and their derivatives. In the centre of its epistemological paradigm was physical measuring becoming something like the “sacrament” of scientific production.
At the same time, this paradigm brought about the end of the ancient student-master relationship between natural sciences and mathematics. In the academic enterprise of today the mathematician only develops the models. It is the physicist (chemist, biologist, geologist) who decides which of the models matches the measurement and gets applied. As a result of this division of labour mathematics was more and more ‘instrumentalised’ and hence isolated from its intellectual source—the natural sciences.
And so it was that physics itself was demoted to a mere interpreter of models and ideas that got completely out of touch with reality – and this to an ever greater extent. To calculate a modern physical model “up to last digit” and to verify it by measurement, today is possible only for the most simplified cases. Physical laws have degenerated to nothing more than hair-splitting; physical facts independent of a model they describe hardly exist anymore.
A Scientific Gold Mine
The scientific division of labour according to the example of large-scale industries also had its positive consequences (“Nothing so bad that it wouldn’t be useful”—an old Russian saying goes). The physical compatibility of completely different mathematical models made it necessary to bring precision of physical measurements to unprecedented heights. Over decades a priceless colossal data base was accumulated. It contains the spectral lines of atoms and molecules, the masses of the elementary particles and atomic nuclei, atomic radii, dimensions, distances, masses and periods of revolution of the planets, moons and asteroids, the physical characteristics of stars and galaxies, and much more. The need for measurements of the highest precision promoted the development of mathematical statistics which in turn made it possible to include precise morphological and sociological data as well as data from evolutionary biology.
Ranging from elementary particles to galactic clusters this scientific data base extends over at least 55 orders of magnitude. Yet, despite its tremendous cosmological significance this data base has never been the object of an integrated (holistic) scientific investigation until 1982. The treasure lying at their feet was not seen by the labour-divided, mega-industrial scientific community.
First indication of the existence of this scientific gold mine came from biology. As the result of 12 years of research Cislenko published his work “Structure of Fauna And Flora With Regard to Body Size of Organisms” (published by Lomonosov-University Moscow, 1980). His work documents what is probably the most important biological discovery in the 20th century. Cislenko was able to prove that segments of increased species representation were repeated on the logarithmic line of body sizes in equal intervals (approx. 0.5 units of the decadic logarithm). The phenomenon is not explicable from a biological point of view. Why should mature individuals of amphibians, reptiles, fish, bird and mammals of different species find it similarly advantageous to have a body size in the range of 8 - 12 cm, 33 - 55 cm or 1,5 - 2,4 m? Cislenko assumed that competition in the plant and animal kingdoms occurs not only for food, water or other resources, but also for the best body sizes. Each species tries to occupy the advantageous intervals on the logarithmic scale where mutual pressure of competition also gave rise to crash zones. Cislenko, however, was not able to explain why both the crash zones and the overpopulated intervals on the logarithmic line are always of the same length and occur in equal distance from each other, nor could he figure out why only certain sizes would be advantageous for the survival of a species and what these advantages actually are.
Cislenko’s work caused the German scientist Dr. Hartmut Müller to search for other scale-invariant distributions in physics, as the phenomenon of scaling has been well known to high-energy physics. In 1982 he was able to prove that there exist statistically identical frequency distributions with logarithmic-periodically recurrent maximums for the masses of atoms and atomic radii as well as for the rest masses and for life spans of elementary particles. Müller found similar frequency distributions along the logarithmic line of the sizes, orbits, masses, and revolution periods of the planets, moons and asteroids. Being a mathematician and physicist he did not fail to recognise the cause for this phenomenon in the existence of a standing pressure wave in the logarithmic space of the scales/measures.
The Logarithmic World of Scales
What actually is scale? Scale is what physics can measure. The result of a physical measurements is always a number with measuring unit, a physical quantity. Say, we have measured 12cm, 33cm and 90cm. Choosing as the standard measure (etalon) 1cm, we will get the number sequence 12 – 33 – 90 (without measurement unit, or as the physicist says: with unit 1). The distances between these numbers on the number line are 33 - 12 = 21 and 90 - 33 = 57. If we were to choose another measuring unit, such as the ell with 49,5cm, the number sequence will be 0,24 – 0,67 – 1,82. The distance between the numbers has changed. It is now 0,67 - 0,24 = 0,42 and 1,82 - 0,667 = 1,16. On the logarithmic line the distance will not change, no matter what measuring unit we choose, it remains constant. In our example, this distance amounts to one unit of the natural logarithm (with radix e = 2,71828…): ln 33 - ln 12 = ln 90 - ln 33 = ln 0,67 - ln 0,24 = ln 1,82 - ln 0,67 = 1. Physical values of measurement therefore own the remarkable feature of logarithmic invariance (scaling). So, in reality any scale is a logarithm.
Now it is interesting, that natural systems are not distributed evenly along the logarithmic line of the scales. There are “attractive” sections which are occupied by a great number of completely different natural systems; and there are “repulsive” sections that most natural systems will avoid. Growing crystals, organisms or populations that reach the limits of such sections on the logarithmic line, will either grow no more or will begin to disintegrate, or else will accelerate growth so as to overcome these sections as quickly as possible.
The institute for Space-Energy-Research i.m. Leonard Euler (IREF) was able to prove the same phenomenon also in demographics (stochastic of world-wide urban populations), economy (stochastic of national product, imports and exports world-wide) and business economy (stochastic of sales volume of large industrial and middle-class enterprises, stochastic of world-wide stock exchange values). The borders of “attractive” and “repulsive” segments on the logarithmic line of scales are easy to find because they recur regularly with a distance of 3 natural logarithmic units. This distance also defines the wavelength of the standing pressure wave: it is 6 units of the natural logarithm.
By its anti-nodes the global standing pressure wave replaces matter on the logarithmic line of scales, and concentrates matter in the node points. Thus, in the transit from wave peak (anti-node) to wave node there occurs a tendency of fusion, while at the transition from node point to anti-node disintegration tendencies arise. This process causes a logarithmic-periodical change of structure. Packed and unpacked systems alternately dominate on the logarithmic line of measures at distances of 3k, i.e. 3, 9, 27, 81 and 243 units of the natural logarithm.
Sound Waves In Logarithmic Space As Cause of Gravitation
The existence of a standing density wave in logarithmic space – for the first time in the history of physics – explains the origin of gravitation. The global flow of matter in direction of the node points of the standing density wave is the reason for the physical phenomenon of gravitational attraction. Thus, particles, atoms, molecules, celestial bodies, etc. – the scales/measures of which stabilise in the node points of the standing pressure wave – become gravitational attractors. In physical reality, therefore, the standing density wave in logarithmic space of scales also manifests as a global standing gravitational wave.
In consequence, the exact identity of value for inert and gravitational masses of physical bodies (as it is claimed by physics today), independent of the body’s density or material, can occur only in the exact node points of the global standing density wave. So far, systematic measurements to verify this postulate of Global-Scaling-Theory have not been carried out. The Institute of Solid-State-Physics at Friedrich Schiller university is now preparing free-fall experiments ( Pseudo-Galileo-Tests) at the Bremen gravity tower in order to determine the possibility of material-related violation of the equivalence principle with a hitherto unmatched precision of < 10-13. The Satellite Test of Equivalence Principle STEP planned for 2004, aspires to an observational limit of ca.10-18. At a height of 550 km comparisons will be made of acceleration velocities of four different pairs of test masses moving on an almost circular solar-synchronous orbit (see: http://einstein.stanford.edu/STEP).
The “Sound Barrier” of the Universe
Standing waves can only form if the medium in which they propagate is bounded. Consequently, the existence of a standing density or pressure wave in the universe means that the universe is limited by scale. At the universe’s lower horizon of scale density of matter reaches a maximum, at its upper horizon a minimum. The two horizons constitute the universe’s “sound barrier”. At precisely these phase transitions pressure waves are reflected, they will overlap and form standing waves. A standing wave can only exist for any length of time if the medium is permanently provided energy from outside. This means that our universe is in a constant energy exchange with other universes.
Standing waves are very common in nature because every medium is limited/bounded, be it the water of the oceans, the air of the earth's atmosphere or the radiation field of the sun’s atmosphere. Standing waves excite the medium into natural oscillations, and due to the fact that the amplitude of a standing wave is no longer time-dependent but only space-dependent, these eigenvibrations will move in sync across the whole medium.
A wave occurs whenever an oscillating particle in a medium excites adjacent particles into vibrations so that the process propagates. Due to the viscosity or elasticity of the medium and the inertia of the particles their oscillation phases differ and the physical effect of a phase shift in space – termed a propagating wave – will arise. The rate of this phase shift (phase velocity) is always finite and dependent on the medium.
In contrast, phase velocity of a standing wave between two adjacent node points is zero because all particles oscillate in phase. This gives rise to the impression that the wave “stands”. In each node point the phase actually bounces 180 degrees – so phase velocity is theoretically infinitely high. It is precisely this property that makes standing waves so attractive for communication.
Standing Waves as Carrier Waves for Information Transmission
Standing waves do not transmit energy, they merely pump energy back and forth within half a wavelength. Half a wavelength is completely sufficient – even for interplanetary communication – if we are dealing with standing waves in logarithmic space. The wavelength of standing density waves in logarithmic space are 2x3k, i.e. 6, 18, 54, 162 and 486 units of the natural logarithm. Half a wavelength, therefore, corresponds to 3, 9, 27, 81 and 243 units. These are relative scales of 1,3 and 3,9 and 11,7 and 35,2 and 105,5 orders of magnitude. Exactly in these intervals node points occur. Hence, node points mark scales relating as 1:20, 1:8103, 1:5,32x1011, 1:1,5x1035 and 1:3,4x10105. Within the scope of these scales communication between two adjacent node points is possible.
The ability to modulate a standing wave is confined to its node points, because it is only in the immediate proximity of the node points that energy can be fed into or taken from a standing wave. If it is a standing wave in linear space, the node points are simply locations in which attachment of an external oscillatory process is possible. Node points of a standing wave in logarithmic space, however, are particular scales which have different frequencies assigned to them. In order to calculate these frequencies it is necessary to acquaint oneself with the mathematical foundations of Global-Scaling-Theory.
The Physics of the Number Line
The world of scales is nothing else but the logarithmic line of numbers known to mathematics at least since the time of Napier (1600). What is new, however, is the fundamental recognition that the number line has a harmonic structure which is itself the cause for the standing pressure wave.
Leonard Euler (1748) had already shown that irrational and transcendental numbers can be uniquely represented as continued fractions in which all elements (numerators and denominators) will be natural numbers. In 1928 Khintchine succeeded to provide the general proof. In the theory of numbers this means that all numbers can be constructed from natural numbers; the universal principle of construction being the continued fraction. All natural numbers 1, 2, 3, 4, 5, … in turn are constructed from prime numbers, these being natural numbers which cannot be further divided without remainder, such as 1, 2, 3, 5, 7, 11, 13, 19, 23, 29, 31, … (traditionally 1 isn’t classed as a prime number although it fulfils all criteria). The distribution of prime numbers on the number line is so irregular that so far no formula was found which would perfectly describe their distribution. Only the Theory of Global Scaling was able to solve this mystery:
The distribution of numbers is indeed very irregular – but only on the linear number line. On the logarithmic number line, large gaps of prime numbers recur in regular intervals. Gauss (1795) had already noticed this. Thus, the set pi(n) of prime numbers up to the number n can be approximated by the simple formula pi(n) = n / ln n. The reason for this phenomenon is the existence of a standing density wave on the logarithmic number line, the node points of this density wave acting as number attractors. This is where prime numbers will ‘accumulate’ and form composite numbers, i.e. non-primes, such as the 7 non-primes from 401 to 409. Hence a “prime number gap” will occur in this place. Precisely where non-primes (i.e. prime clusters) arise on the logarithmic number line, there it is that matter concentrates on the logarithmic line of measures. This isn't magic, it is simply a consequence of the fact that scales are logarithms, i.e. “just” numbers.
So the logarithmic line of scales is nothing else but the logarithmic number line. And because the standing pressure wave is a property of the logarithmic number line, it determines the frequency of distribution of matter on all physically calibrated logarithmic lines – the line of ratios of size, that of masses, of frequencies, of temperatures, velocities, etc.
Now, in order to find a node point on the logarithmic line one only needs the number line (that everybody knows) and a natural standard measure with which to multiply (calibrate) the number line. The wavelength of the standing density wave on the logarithmic number line is known. The distance between adjacent node points is 3 units of the natural logarithm. Thus it is easy to calculate all nodal values Xn by the simple formula Xn = Y x exp(n) (Y being a natural standard measure, n = 0, +-3, +-6, +-9, …).
Frequency values of node points are e.g. 5Hz (n=-54), 101 Hz (n=-51), 2032 Hz (n=-48), 40,8 kHz (n=-45), 820 kHz (n=-42), 16,5 MHz (n=-39), 330,6 MHz (n=-36) etc. The frequency ranges around 5 Hz, 100 Hz, 2 kHz etc. are predestined for energy transmission in finite media. This is also where the carrier frequencies for information transmission in logarithmic space are located. Frequencies that occur near a node point are not just very common in nature but are used also in technological applications.
Natural Standard Measures – The Key to Global Scaling
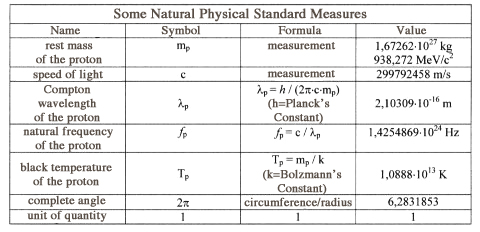
Exact knowledge of the harmonic structure of logarithmic space is the gateway to Global Scaling. In order to open the gate one needs the key –natural standard measures (see table).
Natural standard measures are themselves values of node points. In the node point of a standing wave vibrations do not occur, there is stillness. This is why natural standard measures own a high degree of stability. The rest mass of the proton remains stable over a minimum of 1030 years. For the same reason also the speed of light in a vacuum constitutes a rather obstinate value. The existence of stable natural standard measures is the physical basis of a natural metrology on which Global Scaling Theory is rested.Continued Fractions As “World Formula”
1In 1950 Gantmacher and Krein proved that the spatial distribution of free-moving particles in linear oscillating chain systems can be described by a continued fraction. Terskich (1955) was able to prove the same for non-linear oscillating chain systems. In 1982 Müller showed that the distribution of matter in logarithmic space also has a continued fraction structure. This continued fractional structure provides that the concentration of matter increases hyperbolically in the proximity of node points. In first approximation the distribution of matter in the logarithmic space of scales has the fractal dimension of Cantor dust, but is being deformed hyperbolically in the proximity of a node point (see illustration).
The mathematical aspect is to be found in the realisation that not only is it possible to represent every number as continued fraction, but the distribution of numbers on the logarithmic number line altogether can be represented as such.
This mathematical aspect has immediate physical consequences: Where ever one works with numbers – be it in natural sciences, sociology or economy – one will encounter the phenomenon that there are certain attractor values that all systems, totally independent of their character, prefer, and that the distribution of these attractor values along the logarithmic number line follows a (fractal) continued fraction rule.
This continued fraction rule “contains” physics, chemistry, biology and sociology insofar as these disciplines work with scales (real numbers), i.e. in as far as measurements are made. Many results of complicated, large-scale measurings, therefore, can be relatively easily pre-calculated within the frame of Global Scaling Theory, for example the temperature of cosmic microwave background radiation whose value cannot be larger than Tp x exp(-29) = 2,7696 K; the rest mass of the neutron mn = mp x exp(1/726) = 939,5652 MeV, as well as the rest masses of other elementary particles (see: raum&zeit special 1).
Creation’s Melody
In the context of Global Scaling Theory the hypothesis of the Big Bang appears in a new light. Not a propagating shock wave (pressure wave) in linear space (the echo of the hypothetical primeval explosion) is the cause of cosmic microwave background radiation, but a standing pressure wave in logarithmic space. It is also responsible for the fractal and logarithmic scale-invariant distribution of matter in the entire universe. It created the universe as we know it and recreates it continually. It is the cause of all physical interactions and forces – gravitation, electromagnetism, nuclear fusion and nuclear decay. It is the cause of topological 3-dimensionality of linear space, of left-right-asymmetry, as well as of anisotropy of time. All of these phenomena are physical effects which arise at the transition from logarithmic into linear space. The standing wave in logarithmic space now allows us to communicate across astronomical distances practically without time delay. How is this possible?
Neighbours in Logarithmic Space
Systems in linear space that lie very remote from each other can be very close to each other within the logarithmic space of scales. Our sun and Alpha Centauri are 4 light-years away from each other in linear space, while in the logarithmic space of scales they are immediate neighbours. Once this is understood it is not too difficult to create the physical conditions that will make communication in logarithmic space possible. Two electrons on the same quantum level that may be thousands of kilometres apart, are found in practically one and the same point within the logarithmic space of scales. The fact explains not just a whole range of quantum mechanical phenomena, but constitutes the basis for a totally new telecommunications technology which was publicly demonstrated for the first time on 27th October 2001 in Bad Tölz, Germany.
G-com technology is still in its infancy (a first language modulation succeeded in July of 2001), but in two important aspects it is already far superior to any other conventional means of information transmission. Firstly, a modulated standing gravitational wave can be demodulated in any location on Earth, on planet Mars, or even outside the solar system at the very same moment in time, thus making distances and transmission times meaningless. Secondly, no waves are generated nor transmitted which is why G-com technology does not require aerials, satellites, amplifiers or converters. This launches a new era of telecommunications – free from electric smog.
More information on the Theory of Global Scaling you can find in ‘raum&zeit special 1‘ .
In addition:
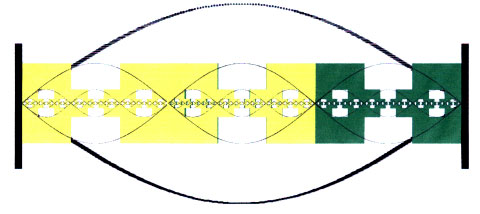
The distribution of matter in the logarithmic space of scales (above) in first approximation has the fractal dimension of Cantor dust (below left), but is deformed hyperbolically in the proximity of a node point (below right).

The continued fractional structure of the distribution of matter in logarithmic space ensures that the concentration of matter in the proximity of the node point increases hyperbolically.

zurück
|